ラグランジュの未定乗数法のわかりやすい考え方

ラグランジュ
f(x,y)
g(x,y)=0

勾配ベクトルはそれぞれ
A(∂f/∂x,∂f/∂y)
B(∂g/∂x,∂g/∂y)

点a,bのまわりの可動方向
C(∂g/∂y,∂g/∂x)

停留点はAとCが垂直に交わる<=>AとBが平行<=>A=λB

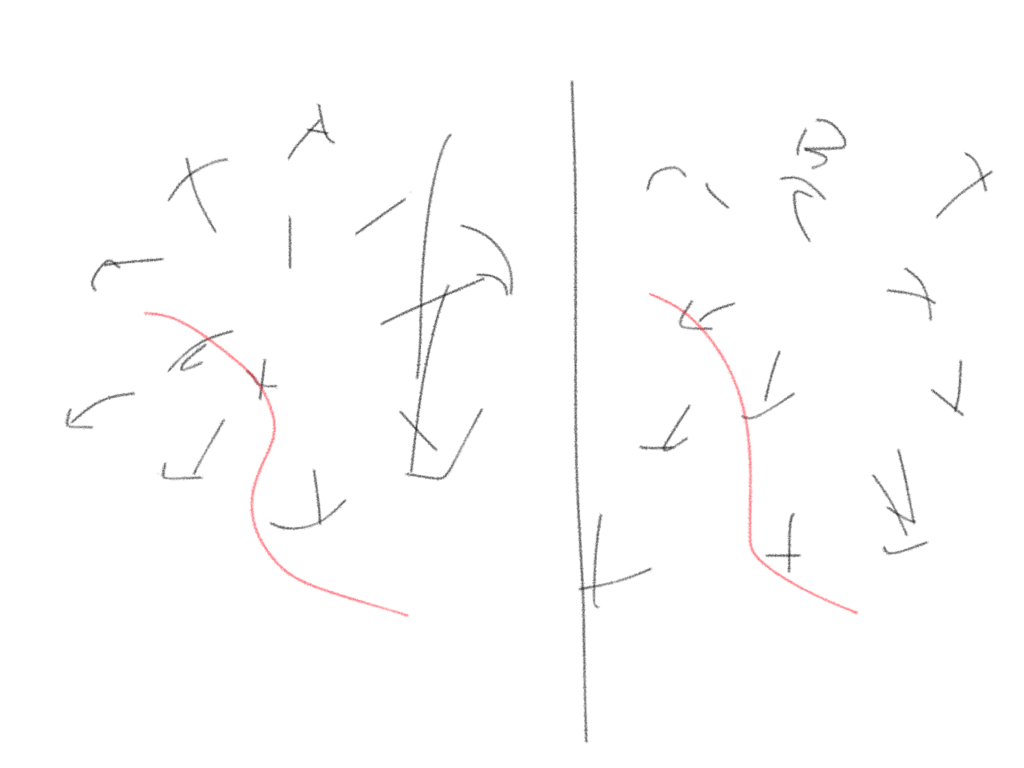
A=λBだけではgが全域なので、
上図のように、fとgの勾配が一致している部分(赤線)がxとyの関係式となってでてくる
ここでg=0条件を加えると

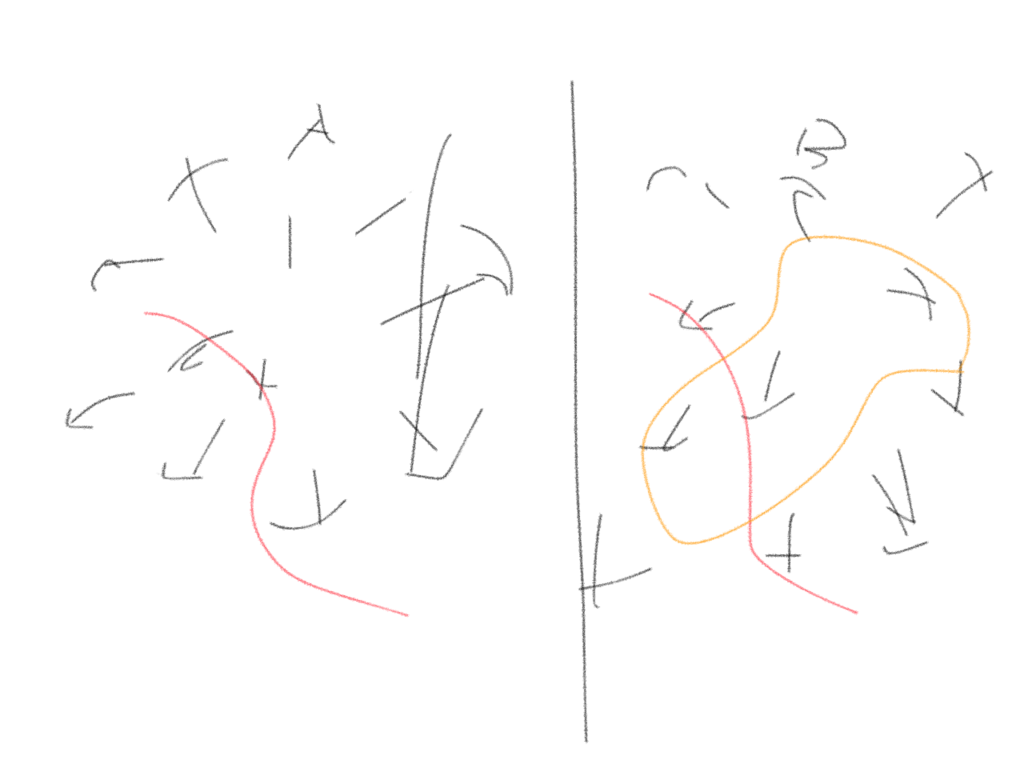
(黄線がg=0の可動域を表す)
fとgが定数倍の関係であるような場合を除いて、黄線と赤線は高々有限個の点で交わり、これが停留点となる
よって我々は次の式をとくことになる

g=0
A=λB

奇しくも、これは

H=f-λgについて
H∂/∂λ=0
H∂/∂x=0
H∂/∂y=0

を解くのと同じである
https://math-note.xyz/analysis/method-of-lagrange-multiplier/