継承したクラスのXmlシリアライズ
インタフェースクラスであるメンバをシリアライズする場合
C# XML serialization of derived classes - Stack Overflow
[XmlInclude(typof(classname))}
インタフェースクラスの要素のリストをシリアライズする場合
d.hatena.ne.jp
[XmlArrayItem(typeof(Concreteclass))]
public List<Interfaceclass>
逆関数法とパストレ
レンダリングにおけるimportance samplingの基礎shikihuiku.wordpress.com
パストレではある点からある方向への放射輝度を計算するときに。球面上の点を一様にサンプリングする必要がある。逆関数法が関係してるのだが、初めて見たときはよくわからんかった。
z軸のサンプリングについて説明する。
1.満たさないといけないもの
z=1-cosΘ
P(Z<=z)=z
2.同値
z=1-cosΘ
P(1-cos日<=1-cosΘ)=1-cosΘ (日は角度の確率変数のつもり)
3.同値
z=1-cosΘ
P(日<=Θ)=1-cosΘ
4.1-cosΘのような乱数を生成したいので、
P(U<=u)=u
からFを作用し
P(F(U)<=x)=1-cosx
をつくることを考える。
5.①P(U<=u)=u
②P(F(U)<=x)=1-cosx
が同時に成り立つとする
6.①より、Pの両辺にFを作用して
P(F(U)<=F(u))=u
7.②においてx=F(u)のとき
P(F(U)<=F(u))=1-cosF(u)
8.6,7の右辺より
u=1-cosF(u)
9.変形
F(u) = arccos(1-u)
これは1-cosxの逆関数である。
4~9までの手順が逆関数法の導出と一致してる。たぶん。
また、球面上のサンプリングにおけるx,yの取り方はもう少し難しい。
レンダリングにおけるimportance samplingの基礎shikihuiku.wordpress.com
気づき
1をみてて、F(T)がF-1で分布するとき、Tは一様分布なんじゃねとおもった。(逆関数法の逆)
(1において、z=1-cosΘでzを一様分布させようとして、9で日=1-cosu になったから)
a[逆関数法]
P(U<=u)=u-> P(F(U)<=x)=F-1(x)
b[逆関数法の逆]
P(F(U)<=x)=F-1(x) -> P(U<=u)=u
逆の証明
同値(左側のPの中身にF-1を作用し、右側のPにFを作用する)
P(U<=F-1(x))=F-1(x) -> P(F(U)<=F(u))=u同値(変数の名前の調整)
P(U<=t)=t -> P(F(U)<=k)=F-1(k) (もともとの逆関数法と主張が一致)
ファッ!?
よって逆関数法は、主張の逆も成り立つ。
これらを使うと以下のことが言える。
一様乱数UにFを作用するとF-1(x)の乱数ができる
Z=G(T)を一様乱数にさせるには、bよりT=G-1(Z)がGで分布するようにすればよい(F=G-1)。TをGで分布させるには、aより(F=G-1)
T=G-1(U)で生成すればよい(Uは一様乱数)
つかいわけていきましょう
C++覚書
Pimpl は デストラクタを隠せ。
ラグランジュの未定乗数法のわかりやすい考え方
ラグランジュ
f(x,y)
g(x,y)=0
勾配ベクトルはそれぞれ
A(∂f/∂x,∂f/∂y)
B(∂g/∂x,∂g/∂y)
点a,bのまわりの可動方向
C(∂g/∂y,∂g/∂x)
停留点はAとCが垂直に交わる<=>AとBが平行<=>A=λB
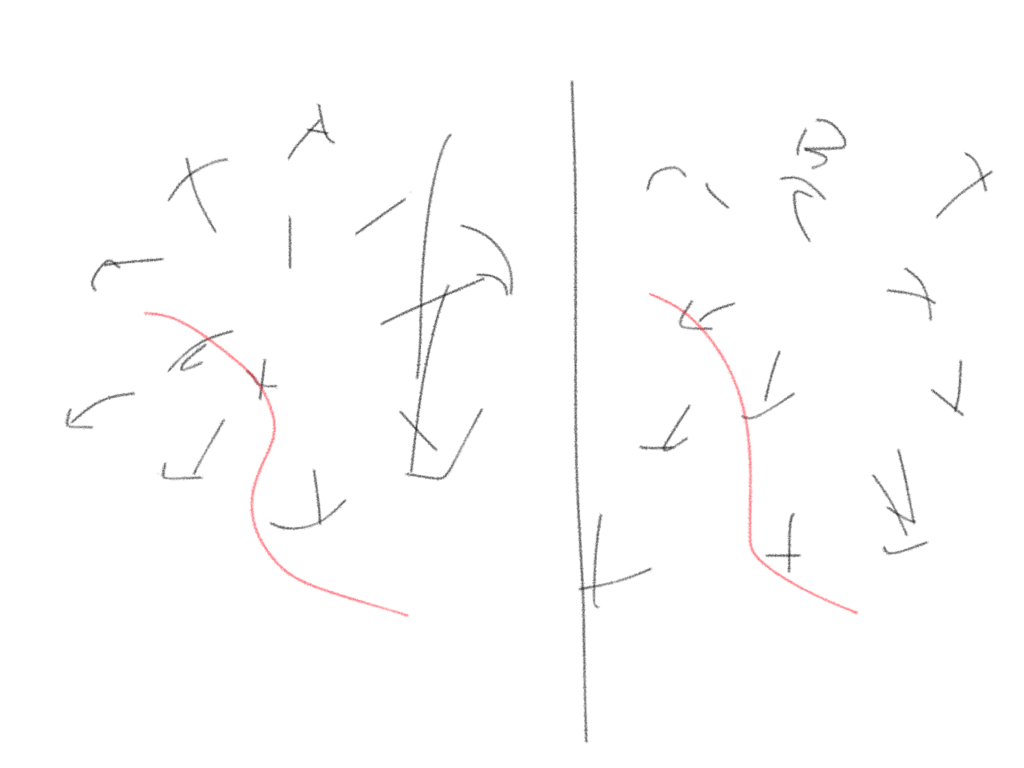
A=λBだけではgが全域なので、
上図のように、fとgの勾配が一致している部分(赤線)がxとyの関係式となってでてくる
ここでg=0条件を加えると
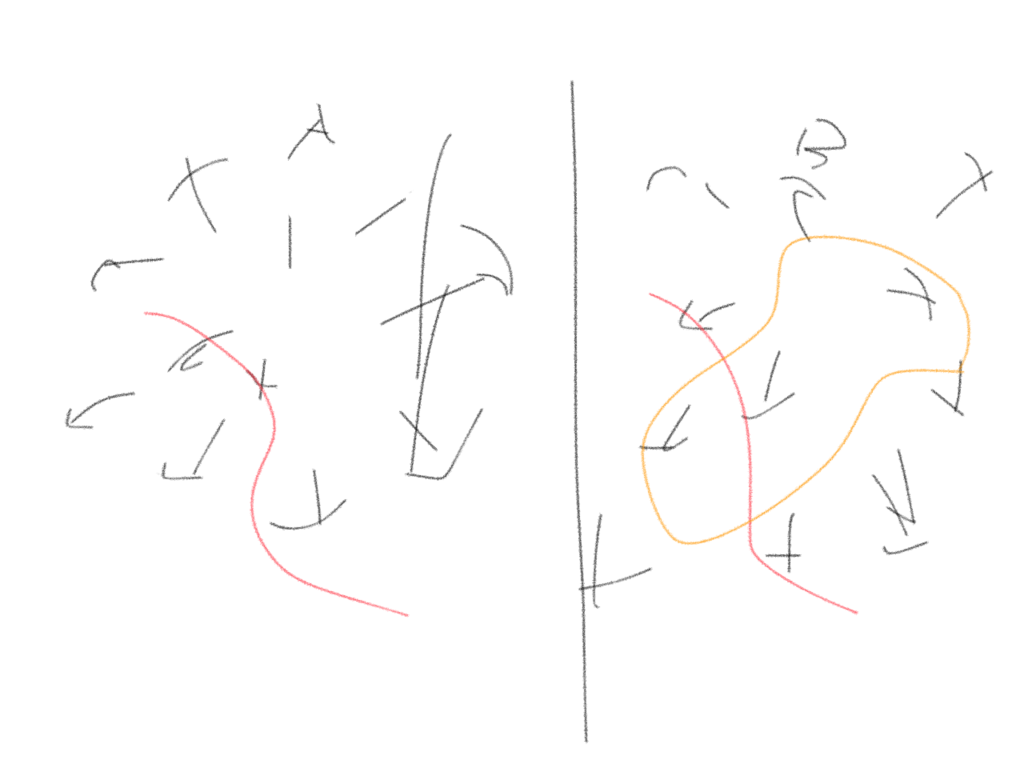
(黄線がg=0の可動域を表す)
fとgが定数倍の関係であるような場合を除いて、黄線と赤線は高々有限個の点で交わり、これが停留点となる
よって我々は次の式をとくことになる
g=0
A=λB
奇しくも、これは
H=f-λgについて
H∂/∂λ=0
H∂/∂x=0
H∂/∂y=0
を解くのと同じである
https://math-note.xyz/analysis/method-of-lagrange-multiplier/
JavaScript覚書
便利なon関数
onresize
canvas
contextとは
getContext() メソッド - Canvasリファレンス - HTML5.JP
drawImageの使い方
drawImage() メソッド - Canvasリファレンス - HTML5.JP
drawImage(image, dx, dy)
drawImage(image, dx, dy, dw, dh)
drawImage(image, sx, sy, sw, sh, dx, dy, dw, dh)
これら3つはそれぞれ、image 引数として HTMLImageElement, HTMLCanvasElement, HTMLVideoElement のいずれかを取ることができます。