心のよりどころなくなった
自作えっちゲームの宣伝のfavが1000を超えた。
学生のころからえっちゲーム制作をしてみたいと思っていて、まずは1000本売り上げようとおもい、既存の作品でそのラインにのっているのはfavが1000以上あるものだったので、まずはそれを目標にしていた。
いつかそっちで飯がくえたらいいなあと漠然と考えつつ大学とか仕事とか人生を過ごしていた。
自分は思った以上にメンタルが弱く結構気持ちが苦しくなることがある。
仕事は周りの方が全然優秀だし、人生設計もしっかりしているし、自立している。
自分は(すごい怠けていたというわけではないが)今の自分ができる範囲で頑張ろう、それでだめならしょうがない、
「まぁ今の手札が全部だめになったら、ゲーム制作する時間がとれるしいっか」と考えることで、苦しみを和らげていた。
急場な時は多少抗不安薬が必要なぐらいメンタルがつらい時もあったが、それでもこの券のことを考えていれば最悪ではなかった。
自分にとってゲーム制作は手札とは関係ない「次の試合への参加券」だった。これを持っている限り、自分の心は安泰だった。
そういう考えで過ごし始めてから10年、ゲーム制作という夢の、最初の目標が今日達成された。
めちゃくちゃ嬉しい。だけどその瞬間から動機が止まらない。今までにない恐怖が襲ってきた。
自分の書いた糞な卒論を発表しないといけなかった日を同じぐらい苦しい。でも原因がわからない。
30分寝ても解決しない。友人に褒めてもらっても(嬉しいけど)心が休まらない。気をそらしたくて何時間もyoutubeやtwitterを見てしまった。
かえって体がどんどん重くなって、動けなくなりそうだった。
ネットの情報を遮断するため銭湯にいって、頭を整理することにした。
現実の恐怖が苦しいとき、ゲーム制作のことについて考えると和らげることができた。でも今日、夢の最初の目標を達成したことで、労力とリターンの計算が現実味を帯びてきて、その輪郭がはっきりしてきた。
そうして「次の試合への参加券」は、今持っている手札と同じ形であることに気づいてしまった。
言語化できたことで幾分は楽になった。それでもこれからの絶望は計り知れない。
自分は今から、10年間なぁなぁで切ってきたこの手札に、真正面から向き合わなければならない。その恐怖に耐えきれるだろうか。
もう一つの券も学生のころから持っている。使いたくなくて見ないようにしていたけど、今後恐怖に負けた時はこれに頼らざるをえないかもしれない。
「北欧に健康な人間でも安楽死させてくれる組織があるらしい」。
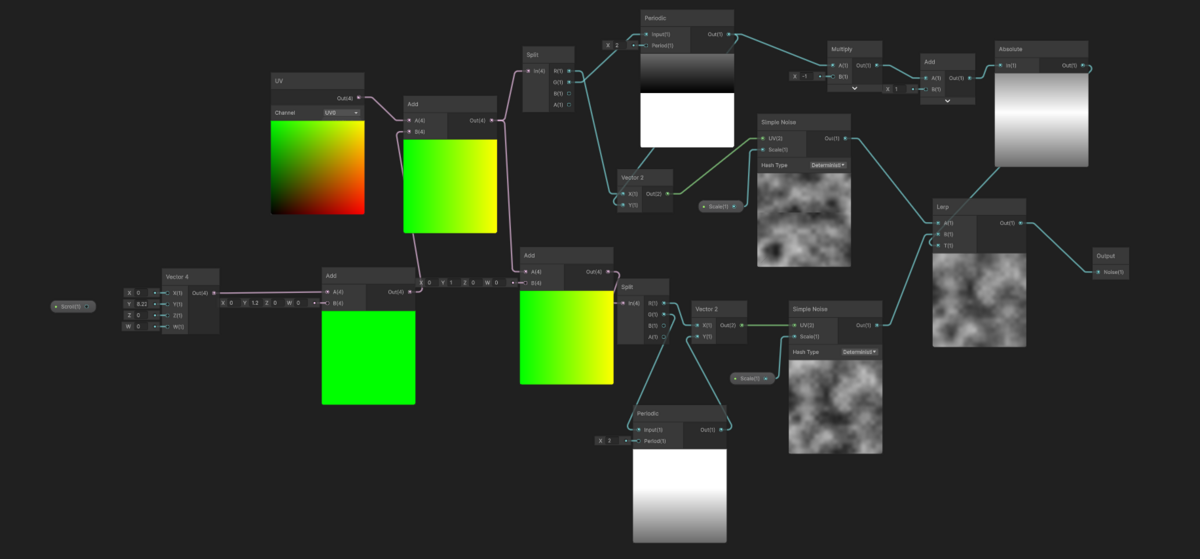
UnityVFXで極座標ノイズをつくる
youtu.be
ノイズテクスチャに極座標ノードを付けて同心円状のノイズを作っているのを見た。
VFXの勉強がてらこれをやってみた
動画ではノイズテクスチャをつっていたが、面倒だったのでノイズノードを使おうとした。
テクスチャの代わりにノイズノードにつけたが、画面下半分に縦線が入る
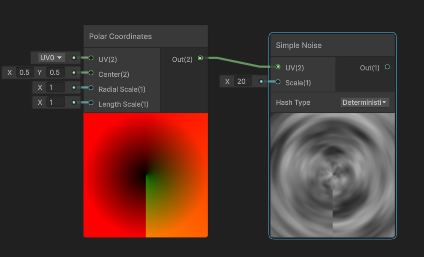
縦線の右側がuv.y=0.5、左側がuv.y=-0.5になっている
この縦線をまたいでもきれいにつながってほしい。
つまりノイズの方を常に「noise(y)=noise(y+1)」というなるようなものを作れば、極座標ノードにつけてもきれいに渦巻っぽいノイズになるはず
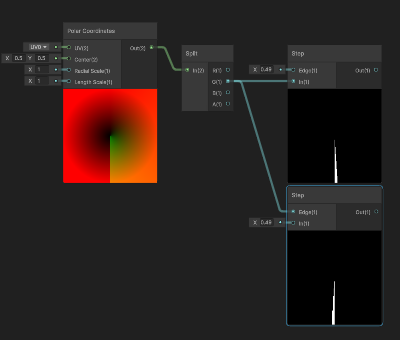
単に「周期1で繰り返す」ノイズではだめで、切れ目ができてしまう
そこで周期2のノイズを用意(noise_2と呼ぶ、y=2->0の時に切れ目がある)し、
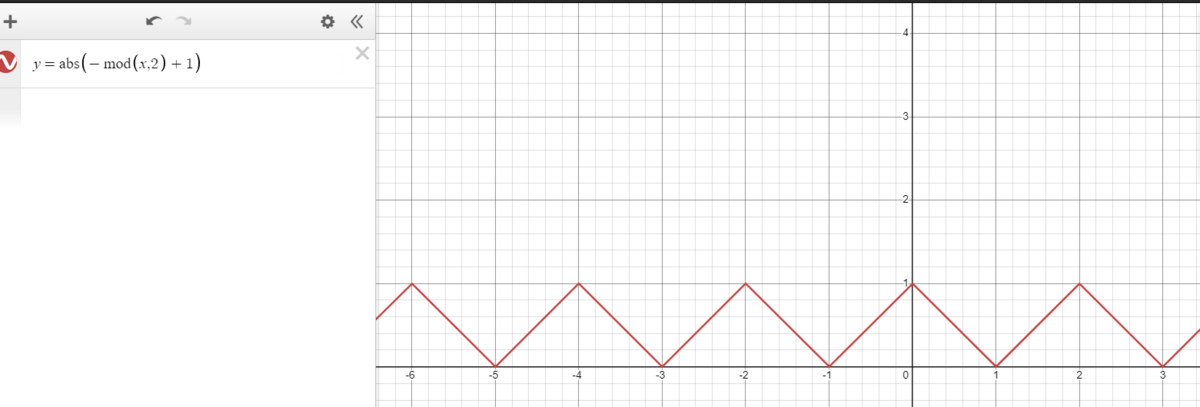
output = lerp ( (noise_2(y+1) , noise_2(y), t) (ただし t=abs(-mod(y,2)+1))
y=0のとき、t=1, noise_2(y+1) = noise_2(1) の比重がおおきいので切れ目がない
y=1のとき、t=0, noise_2(y) = noise_2(1) の比重がおおきいので切れ目がない
y=2のとき、t=1, noise_2(y+1) = noise_2(1) の比重がおおきいので切れ目がない
という風に、切れ目のないほうの比重が大きくなるようにできる
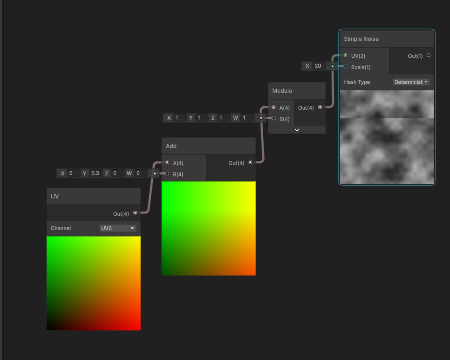
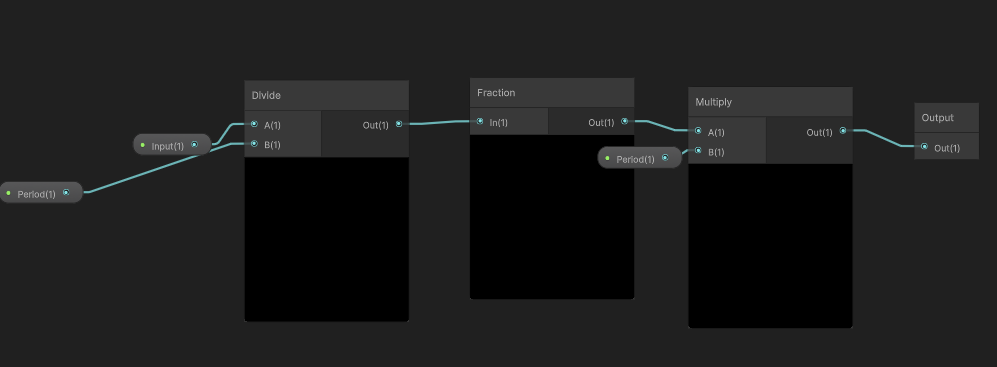
modの部分はmoduloにしたかったが、負の数をいい感じにしてくれないので代わりにperiodicていうサブグラフ作った
こうして、「y方向に周期1できれいにつながるノイズ」がでいたので、YLoopNoiseと名付けて、極座標ノードにつけてみた
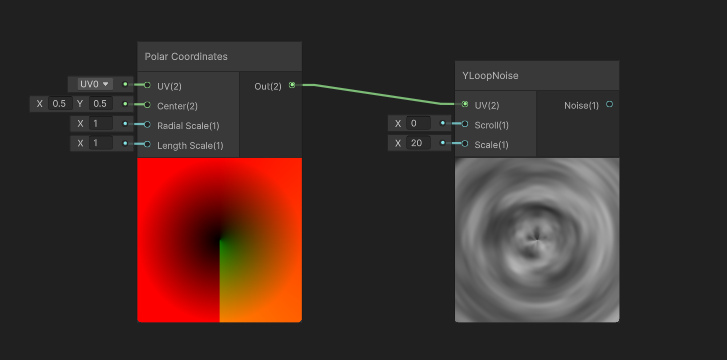
予想どおりノイズ下半分の縦線がなくなった
Unity 2Dレンダラで3Dオブジェクトをライティングする
qiita.com
ノーマルマップがないモデルだといい感じにライティングされなかったからこれ多分モデルにノーマルマップがあるときの事例だと思う(未検証)
頂点のノーマルだけで事足りる場合もあるのでちょっと改変した
〜 shader "Universal Render Pipeline/2D/Sprite-Lit-3D" { Properties { [MainTexture] _MainTex("Diffuse", 2D) = "white" {} [MainColor] _BaseColor("Color", Color) = (1,1,1,1) [HDR] _EmissionColor("Emission", Color) = (0,0,0,0) _MaskTex("Mask", 2D) = "white" {} _NormalMap("Normal Map", 2D) = "bump" {} // Legacy properties. They're here so that materials using this shader can gracefully fallback to the legacy sprite shader. [HideInInspector] _Color("Tint", Color) = (1,1,1,1) [HideInInspector] _RendererColor("RendererColor", Color) = (1,1,1,1) [HideInInspector] _Flip("Flip", Vector) = (1,1,1,1) [HideInInspector] _AlphaTex("External Alpha", 2D) = "white" {} [HideInInspector] _EnableExternalAlpha("Enable External Alpha", Float) = 0 } HLSLINCLUDE #include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl" ENDHLSL SubShader { Tags {"Queue" = "Geometry" "RenderType" = "Opacue" "RenderPipeline" = "UniversalPipeline" } Blend SrcAlpha OneMinusSrcAlpha Cull Back ZWrite On Pass { Tags { "LightMode" = "Universal2D" } HLSLPROGRAM #pragma prefer_hlslcc gles #pragma vertex CombinedShapeLightVertex #pragma fragment CombinedShapeLightFragment #pragma multi_compile USE_SHAPE_LIGHT_TYPE_0 __ #pragma multi_compile USE_SHAPE_LIGHT_TYPE_1 __ #pragma multi_compile USE_SHAPE_LIGHT_TYPE_2 __ #pragma multi_compile USE_SHAPE_LIGHT_TYPE_3 __ struct Attributes { float3 positionOS : POSITION; float4 color : COLOR; float2 uv : TEXCOORD0; }; struct Varyings { float4 positionCS : SV_POSITION; float4 color : COLOR; float2 uv : TEXCOORD0; float2 lightingUV : TEXCOORD1; }; #include "Packages/com.unity.render-pipelines.universal/Shaders/2D/Include/LightingUtility.hlsl" TEXTURE2D(_MainTex); SAMPLER(sampler_MainTex); TEXTURE2D(_MaskTex); SAMPLER(sampler_MaskTex); TEXTURE2D(_NormalMap); SAMPLER(sampler_NormalMap); half4 _MainTex_ST; half4 _NormalMap_ST; half4 _BaseColor; half4 _EmissionColor; #if USE_SHAPE_LIGHT_TYPE_0 SHAPE_LIGHT(0) #endif #if USE_SHAPE_LIGHT_TYPE_1 SHAPE_LIGHT(1) #endif #if USE_SHAPE_LIGHT_TYPE_2 SHAPE_LIGHT(2) #endif #if USE_SHAPE_LIGHT_TYPE_3 SHAPE_LIGHT(3) #endif Varyings CombinedShapeLightVertex(Attributes v) { Varyings o = (Varyings)0; o.positionCS = TransformObjectToHClip(v.positionOS); o.uv = TRANSFORM_TEX(v.uv, _MainTex); float4 clipVertex = o.positionCS / o.positionCS.w; o.lightingUV = ComputeScreenPos(clipVertex).xy; o.color = v.color * _BaseColor; return o; } #include "Packages/com.unity.render-pipelines.universal/Shaders/2D/Include/CombinedShapeLightShared.hlsl" half4 CombinedShapeLightFragment(Varyings i) : SV_Target { half4 main = i.color * SAMPLE_TEXTURE2D(_MainTex, sampler_MainTex, i.uv); half4 mask = SAMPLE_TEXTURE2D(_MaskTex, sampler_MaskTex, i.uv); return CombinedShapeLightShared(main, mask, i.lightingUV)+main*_EmissionColor; } ENDHLSL } Pass { Tags { "LightMode" = "NormalsRendering"} HLSLPROGRAM #pragma prefer_hlslcc gles #pragma vertex NormalsRenderingVertex #pragma fragment NormalsRenderingFragment struct Attributes { float3 positionOS : POSITION; float3 normalOS : NORMAL;//ここで頂点の法線を取得 float4 color : COLOR; float2 uv : TEXCOORD0; float4 tangent : TANGENT; }; struct Varyings { float4 positionCS : SV_POSITION; float4 color : COLOR; float2 uv : TEXCOORD0; float3 normalWS : TEXCOORD1; float3 tangentWS : TEXCOORD2; float3 bitangentWS : TEXCOORD3; }; TEXTURE2D(_MainTex); SAMPLER(sampler_MainTex); TEXTURE2D(_NormalMap); SAMPLER(sampler_NormalMap); float4 _NormalMap_ST; // Is this the right way to do this? Varyings NormalsRenderingVertex(Attributes attributes) { Varyings o = (Varyings)0; o.positionCS = TransformObjectToHClip(attributes.positionOS); o.uv = TRANSFORM_TEX(attributes.uv, _NormalMap); o.uv = attributes.uv; o.color = attributes.color; o.normalWS = TransformObjectToWorldDir(attributes.normalOS); o.tangentWS = TransformObjectToWorldDir(attributes.tangent.xyz); o.bitangentWS = cross(o.normalWS, o.tangentWS) * attributes.tangent.w; return o; } #include "Packages/com.unity.render-pipelines.universal/Shaders/2D/Include/NormalsRenderingShared.hlsl" float4 NormalsRenderingFragment(Varyings i) : SV_Target { float4 mainTex = i.color * SAMPLE_TEXTURE2D(_MainTex, sampler_MainTex, i.uv); float3 normalTS = UnpackNormal(SAMPLE_TEXTURE2D(_NormalMap, sampler_NormalMap, i.uv)); //return NormalsRenderingShared(mainTex, normalTS, i.tangentWS.xyz, i.bitangentWS.xyz, i.normalWS.xyz); half3 normalVS = TransformWorldToViewDir(i.normalWS.xyz);//頂点の法線情報をそのまま使う half4 normalColor; normalColor.rgb = 0.5 * ((normalVS)+1); normalColor.a = i.color.a; // used for blending return normalColor; } ENDHLSL } Pass { Tags { "LightMode" = "UniversalForward" "Queue"="Geometry" "RenderType"="Opacue"} HLSLPROGRAM #pragma prefer_hlslcc gles #pragma vertex UnlitVertex #pragma fragment UnlitFragment struct Attributes { float3 positionOS : POSITION; float4 color : COLOR; float2 uv : TEXCOORD0; }; struct Varyings { float4 positionCS : SV_POSITION; float4 color : COLOR; float2 uv : TEXCOORD0; }; TEXTURE2D(_MainTex); SAMPLER(sampler_MainTex); float4 _MainTex_ST; Varyings UnlitVertex(Attributes attributes) { Varyings o = (Varyings)0; o.positionCS = TransformObjectToHClip(attributes.positionOS); o.uv = TRANSFORM_TEX(attributes.uv, _MainTex); o.uv = attributes.uv; o.color = attributes.color; return o; } float4 UnlitFragment(Varyings i) : SV_Target { float4 mainTex = i.color * SAMPLE_TEXTURE2D(_MainTex, sampler_MainTex, i.uv); return mainTex; } ENDHLSL } } FallBack "Universal Render Pipeline/Unlit" } 〜
Tags { "LightMode" = "NormalsRendering"}
のPassで
頂点シェーダで法線情報をもらって
NormalsRenderingFragmentでそのままつかっただけ

白いCubeは3dモデルだけど松明のLight2D(PointLight)の光を受けている
パストレ
#### PBR本とソースコード
ソースコード github.com
#### パストレ確率論解説
uraymarchingメモ
- http://tips.hecomi.com/entry/2018/12/31/211448
- GitHub - hecomi/uRaymarching: Raymarching Shader Generator in Unity
- Raymarching.cginc
コード例
- レンダリングパスでスイッチングする部分(https://github.com/hecomi/uRaymarching/blob/a2574b027203b4388234679dcb567dcc9ecc21af/Assets/uRaymarching/Shaders/Include/Legacy/DeferredStandard.cginc)
#ifndef VERT_FRAG_DEFERRED_OBJECT_STANDARD_H #define VERT_FRAG_DEFERRED_OBJECT_STANDARD_H #include "UnityCG.cginc" #include "Lighting.cginc" #include "UnityPBSLighting.cginc" #include "./Structs.cginc" #include "./Raymarching.cginc" #include "./Utils.cginc" int _Loop; float _MinDistance; fixed4 _Color; float _Glossiness; float _Metallic; #ifdef FULL_SCREEN struct v2f { float4 pos : SV_POSITION; float4 projPos : TEXCOORD0; float4 lmap : TEXCOORD1; #ifdef LIGHTMAP_OFF #if UNITY_SHOULD_SAMPLE_SH half3 sh : TEXCOORD2; #endif #endif }; #else struct v2f { float4 pos : SV_POSITION; float3 worldPos : TEXCOORD0; float3 worldNormal : TEXCOORD1; float4 projPos : TEXCOORD2; float4 lmap : TEXCOORD3; #ifdef LIGHTMAP_OFF #if UNITY_SHOULD_SAMPLE_SH half3 sh : TEXCOORD4; #endif #endif }; #endif v2f Vert(appdata_full v) { v2f o; #ifdef FULL_SCREEN o.pos = v.vertex; #else o.pos = UnityObjectToClipPos(v.vertex); o.worldPos = mul(unity_ObjectToWorld, v.vertex); o.worldNormal = UnityObjectToWorldNormal(v.normal); #endif o.projPos = ComputeNonStereoScreenPos(o.pos); COMPUTE_EYEDEPTH(o.projPos.z); #ifndef DYNAMICLIGHTMAP_OFF o.lmap.zw = v.texcoord2.xy * unity_DynamicLightmapST.xy + unity_DynamicLightmapST.zw; #else o.lmap.zw = 0; #endif #ifndef LIGHTMAP_OFF o.lmap.xy = v.texcoord1.xy * unity_LightmapST.xy + unity_LightmapST.zw; #else o.lmap.xy = 0; #ifndef SPHERICAL_HARMONICS_PER_PIXEL #if UNITY_SHOULD_SAMPLE_SH o.sh = 0; o.sh = ShadeSHPerVertex(o.worldNormal, o.sh); #endif #endif #endif return o; } GBufferOut Frag(v2f i, GBufferOut o) { RaymarchInfo ray; INITIALIZE_RAYMARCH_INFO(ray, i, _Loop, _MinDistance); Raymarch(ray); #ifdef USE_RAYMARCHING_DEPTH o.depth = ray.depth; #endif float3 worldPos = ray.endPos; float3 worldNormal = 2.0 * ray.normal - 1.0; fixed3 worldViewDir = normalize(UnityWorldSpaceViewDir(worldPos)); SurfaceOutputStandard so; UNITY_INITIALIZE_OUTPUT(SurfaceOutputStandard, so); so.Albedo = _Color.rgb; so.Metallic = _Metallic; so.Smoothness = _Glossiness; so.Emission = 0.0; so.Alpha = _Color.a; so.Occlusion = 1.0; so.Normal = worldNormal; #ifdef POST_EFFECT POST_EFFECT(ray, so); #endif UnityGI gi; UNITY_INITIALIZE_OUTPUT(UnityGI, gi); gi.indirect.diffuse = 0; gi.indirect.specular = 0; gi.light.color = 0; gi.light.dir = half3(0, 1, 0); gi.light.ndotl = LambertTerm(worldNormal, gi.light.dir); UnityGIInput giInput; UNITY_INITIALIZE_OUTPUT(UnityGIInput, giInput); giInput.light = gi.light; giInput.worldPos = worldPos; giInput.worldViewDir = worldViewDir; giInput.atten = 1; #if defined(LIGHTMAP_ON) || defined(DYNAMICLIGHTMAP_ON) giInput.lightmapUV = i.lmap; #else giInput.lightmapUV = 0.0; #endif #if UNITY_SHOULD_SAMPLE_SH #ifdef SPHERICAL_HARMONICS_PER_PIXEL giInput.ambient = ShadeSHPerPixel(worldNormal, 0.0, worldPos); #else giInput.ambient.rgb = i.sh; #endif #else giInput.ambient.rgb = 0.0; #endif giInput.probeHDR[0] = unity_SpecCube0_HDR; giInput.probeHDR[1] = unity_SpecCube1_HDR; #if UNITY_SPECCUBE_BLENDING || UNITY_SPECCUBE_BOX_PROJECTION giInput.boxMin[0] = unity_SpecCube0_BoxMin; // .w holds lerp value for blending #endif #if UNITY_SPECCUBE_BOX_PROJECTION giInput.boxMax[0] = unity_SpecCube0_BoxMax; giInput.probePosition[0] = unity_SpecCube0_ProbePosition; giInput.boxMax[1] = unity_SpecCube1_BoxMax; giInput.boxMin[1] = unity_SpecCube1_BoxMin; giInput.probePosition[1] = unity_SpecCube1_ProbePosition; #endif LightingStandard_GI(so, giInput, gi); o.emission = LightingStandard_Deferred(so, worldViewDir, gi, o.diffuse, o.specular, o.normal); #ifndef UNITY_HDR_ON o.emission.rgb = exp2(-o.emission.rgb); #endif UNITY_OPAQUE_ALPHA(o.diffuse.a); return o; } #endif
- エディタからコード生成されるもの(生成元はhttps://github.com/hecomi/uRaymarching/blob/a2574b027203b4388234679dcb567dcc9ecc21af/Assets/uRaymarching/Editor/Resources/ShaderTemplates/uRaymarching/Deferred/Standard.txt )
Shader "Raymarching/Forward_HexFloor" { Properties { [Header(PBS)] _Color("Color", Color) = (1.0, 1.0, 1.0, 1.0) _Metallic("Metallic", Range(0.0, 1.0)) = 0.5 _Glossiness("Smoothness", Range(0.0, 1.0)) = 0.5 [Header(Pass)] [Enum(UnityEngine.Rendering.CullMode)] _Cull("Culling", Int) = 2 [Header(Raymarching)] _Loop("Loop", Range(1, 100)) = 30 _MinDistance("Minimum Distance", Range(0.001, 0.1)) = 0.01 _DistanceMultiplier("Distance Multiplier", Range(0.001, 2.0)) = 1.0 [PowerSlider(10.0)] _NormalDelta("NormalDelta", Range(0.00001, 0.1)) = 0.0001 // @block Properties [Header(Additional Properties)] _TopColor("TopColor", Color) = (1, 1, 1, 0) // @endblock } SubShader { Tags { "RenderType" = "Opaque" "Queue" = "Geometry" "DisableBatching" = "True" } Cull [_Cull] CGINCLUDE #define OBJECT_SHAPE_CUBE #define USE_RAYMARCHING_DEPTH #define SPHERICAL_HARMONICS_PER_PIXEL #define DISTANCE_FUNCTION DistanceFunction #define POST_EFFECT PostEffect #define PostEffectOutput SurfaceOutputStandard #include "Assets\uRaymarching\Shaders\Include\Legacy/Common.cginc" // @block DistanceFunction inline float DistanceFunction(float3 pos) { // combine even hex tiles and odd hex tiles float radius = 0.2; float space = 0.1; float wave = 0.1; float3 objectScale = GetScale(); float height = objectScale.y * 0.5 - wave; float3 scale = objectScale * 0.5; float pitch = radius * 2 + space; float3 offset = float3(pitch * 0.5, 0.0, pitch * 0.866); float3 loop = float3(offset.x * 2, 1.0, offset.z * 2); float3 p1 = pos; float3 p2 = pos + offset; // calculate indices float2 pi1 = floor(p1 / loop).xz; float2 pi2 = floor(p2 / loop).xz; pi1.y = pi1.y * 2 + 1; pi2.y = pi2.y * 2; p1 = Repeat(p1, loop); p2 = Repeat(p2, loop); // draw hexagonal prisms with random heights float dy1 = wave * sin(10 * Rand(pi1) + 5 * PI * _Time.x); float dy2 = wave * sin(10 * Rand(pi2) + 5 * PI * _Time.x); float d1 = HexagonalPrismY(float3(p1.x, pos.y + dy1, p1.z), float2(radius, height)); float d2 = HexagonalPrismY(float3(p2.x, pos.y + dy2, p2.z), float2(radius, height)); // maximum indices loop.z *= 0.5; float2 mpi1 = floor((scale.xz + float2(space * 0.5, radius)) / loop.xz); float2 mpi2 = floor((scale.xz + float2(radius + space, radius)) / loop.xz); // remove partial hexagonal prisms // if (pi1.x >= mpi1.x || pi1.x < -mpi1.x) d1 = max(d1, space); // if (pi1.y >= mpi1.y || pi1.y <= -mpi1.y) d1 = max(d1, space); float o1 = any( step(mpi1.x, pi1.x) + step(pi1.x + 1, -mpi1.x) + step(mpi1.y, abs(pi1.y))); d1 = o1 * max(d1, 0.1) + (1 - o1) * d1; // if (!all(max(mpi2 - abs(pi2), 0.0))) d2 = max(d2, space); float o2 = any(step(mpi2, abs(pi2))); d2 = o2 * max(d2, 0.1) + (1 - o2) * d2; // combine //return min(d1, d2); return d1; } // @endblock // @block PostEffect float4 _TopColor; inline void PostEffect(RaymarchInfo ray, inout PostEffectOutput o) { float3 localPos = ToLocal(ray.endPos); o.Emission += smoothstep(0.48, 0.50, localPos.y) * _TopColor; o.Occlusion *= 1.0 - 1.0 * ray.loop / ray.maxLoop; } // @endblock ENDCG Pass { Tags { "LightMode" = "Deferred" } Stencil { Comp Always Pass Replace Ref 128 } CGPROGRAM #include "Assets\uRaymarching\Shaders\Include\Legacy/DeferredStandard.cginc" #pragma target 3.0 #pragma vertex Vert #pragma fragment Frag #pragma exclude_renderers nomrt #pragma multi_compile_prepassfinal #pragma multi_compile ___ UNITY_HDR_ON ENDCG } } Fallback "Raymarching/Fallbacks/StandardSurfaceShader" CustomEditor "uShaderTemplate.MaterialEditor" }
仕組み
- vertexシェーダでprojPosにComputeNonStereoScreenPosでスクリーン上の座標を入れとくことで後のポストエフェクトに使いやすくしている(利便性のためzはEYE_DEPTHを適用してビュー空間上の深度に変換している。)
- PostEffect関数で返すべきデータの種類がレンダリングモードに応じて適切に選択できるように、PostEffectOutputをdefineしている(どう変わるかはhttps://github.com/hecomi/uRaymarching/blob/master/Documents/Legacy.md のPostEffectを参照)